Algorytmy monero część 1

Poniższy artykuł jest napisany w oparciu o opracowanie

"Understanding Monero Cryptography, Privacy" autorstwa @luigi1111

Hasło przewodnie Monero brzmi "Secure, Private, Untraceable", czyli "Bezpieczny, prywatny, nie do wyśledzenia". Bezpiczeństwo może odnosić się do wielu aspektów kryptowalut, ale tutaj jesteśmy szczególnie zainteresowani tylko bezpieczeństwem związanym z prywatnością/anonimowością.

Czym jest Kryptografia Krzywej Eliptycznej?

Dobrze, więc czym jest ECC? Z Wikipedii: " Elliptic curve cryptography (ECC) to podejście do kryptografii z kluczem publicznym oparte na algebraicznej strukturze krzywych eliptycznych nad skończonymi polami. "

A teraz, co to znaczy? Nie mam pojęcia...

A tak bardziej poważnie, to przejdźmy przez to:

Public-Key Cryptography, czyli kryptografia asymetryczna, używa pary kluczy zamiast pojedynczego klucza prywatnego, jak w kryptografii symetrycznej (np. AES): klucza publicznego, który jest rozdawany "światu"; i klucza prywatnego, który ma być zawsze utrzymywany w tajemnicy. Aby rozwiązanie było bezpieczne, musi być trudno rozgryźć klucz prywatny biorąc pod uwagę klucz publiczny; aby było użyteczne, musi być łatwo obliczyć klucz publiczny biorąc pod uwagę klucz prywatny. ECC opiera swoje bezpieczeństwo na ECDLP.

Wnioski: dla pary kluczy publiczny/prywatny przejście prywatny->publiczny jest łatwe, ale publiczny->prywatny jest "niemożliwe".

"Struktura algebraiczna krzywych eliptycznych": Co to jest? Jest to krzywa płaska spełniająca równanie y^2 = x^3 + ax + b, która może wyglądać tak:

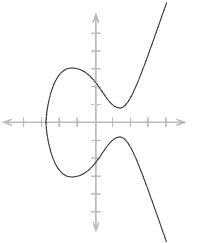krzywa eliptyczna

Czy ma to jakieś znaczenie? Raczej nie ale na wypadek, gdyby ktoś był zainteresowany, istnieje mnóstwo artykułów (wiele związanych z Bitcoinem) tam, które szczegółowo wyjaśniają, jak działają krzywe eliptyczne, np. tu, tu i tutaj.

Wnioski: żadne, ta śmiesznie wyglądająca krzywa nie pomoże ci zrozumieć i nie jest nawet jak wygląda krzywa Monero :-)

"nad skończonymi polami": oznacza to po prostu, że punkty krzywej są brane modulo jakiejś (dużej, pierwszej) liczby. Wszyscy znają przynajmniej dodawanie i odejmowanie modulo (nawet jeśli nigdy nie słyszeli tego słowa) ze względu na naszą ewidencję czasu. Jeśli jest 10 rano, to która godzina będzie za 5 godzin? Gratulacje, właśnie wykonałeś dodawanie modulo. Krzywa eliptyczna na skończonym polu może wyglądać tak:

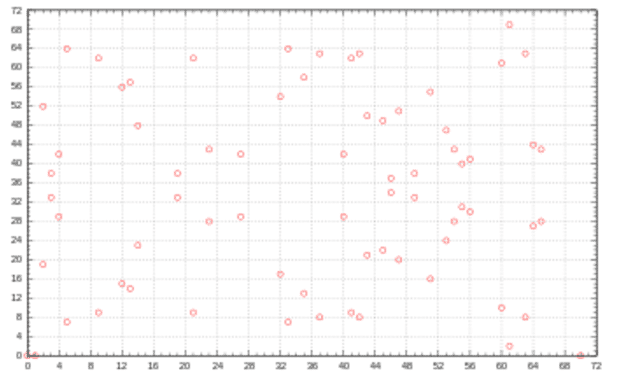krzywa eliptyczna na skończonym polu - przykład

Whoa, to wygląda dziwnie. Tak, to prawda. Wnioski: żadne. Zauważ, jak punkty są "odbite" od niewidzialnej linii w środku.

Podstawową korzyścią z używania ECC vs czegoś takiego jak RSA jest to, że klucze są znacznie mniejsze dla podobnych poziomów bezpieczeństwa.

Jedyne rzeczy, które musisz wiedzieć, aby kontynuować, to:

• Punkt na krzywej może być dodany do lub odjęty od innego punktu, lub samego siebie.
• Punkt nie może być pomnożony lub podzielony przez inny punkt.
• Dodanie punktu do siebie pozwala na "skalarne mnożenie", czyli to, gdzie dzieje się magia.

Odejmowanie punktu od siebie nie jest zbyt użyteczne, ponieważ zwróci ECC odpowiednik 0. Dzielenie przez liczbę całkowitą nie jest możliwe (równoważna operacja modulo - modularny odwrotnik multiplikatywny - jest możliwa, ale tylko przy znajomości oryginalnego skalara).

Mnożenie skalarne to po prostu dodawanie punktu do siebie wiele razy; biorąc pod uwagę punkt A, 5A = A + A + A + A + A. Ponieważ używamy astronomicznie dużych skalarów, aby zapobiec łatwemu brute-forcingowi, używamy technik takich jak double-and-add (podwój i dodaj), aby umożliwić obliczenia w czasie zbliżonym do logarytmicznego (tj. naprawdę szybko!). Szybki przykład:

Załóżmy, że naszym skalarem jest 27, a my chcemy obliczyć 27A. Używając najprostszej "naiwnej" metody, potrzebowalibyśmy 26 dodawania. Zamiast tego wykonujemy:

1. Dodaj A do siebie: 2A. Nazwijmy ten nowy punkt B.
2. Dodaj B do siebie: 2B = 4A = C.
3. Dodaj C do siebie: 2C = 4B = 8A = D.
4. Dodaj D do siebie: 2D = 4C = 8B = 16A = E.
5. Dodaj D do E: 24A = F.
6. Dodaj B do F: 26A = G.
7. Dodaj A do G: 27A

Udało nam się zredukować 26 operacji dodawania do 7. Różnica rośnie wykładniczo przy większych skalarach. Różnica prędkości dla średniej wielkości skalara jest czymś pomiędzy "cała energia we wszechświecie nie jest wystarczająca" i "zajmuje mniej niż 1/100 sekundy na przeciętnym komputerze", co jest interesujące do rozważenia.

To tyle jeśli chodzi o ogólne rzeczy związane z ECC! Jeśli chcesz bardziej dogłębnych szczegółów technicznych, zobacz linki powyżej. :)

Krzywa Monero oraz prywatne i publiczne "klucze"

Teraz, na rzeczy specyficzne dla Monero. Na koniec.

Najpierw trochę nudnych rzeczy jak stałe krzywej. W dokumentacji Cryptonote (protokołu wykorzystywanego przez Monero) czytamy:

Mamy do czynienia z krzywą Ed25519, która jest skręconą krzywą Edwardsa.

Prześledźmy to szybko:

• q: jest to całkowita liczba punktów na tej krzywej. Dla naszych celów jest ona w większości przypadków nieistotna.
• d: pierwiastek używany w równaniu krzywej poniżej. Nieistotny.
• E: równanie dla naszej krzywej Ed25519. Wow, błyszczące! Nieważne.
• G: punkt bazowy lub punkt generatora. To jest ważne! Jest to baza, od której zaczyna się wiele operacji. Jest to "A" w powyższym przykładzie. W hexie, w którym wszystkie nasze klucze są powszechnie reprezentowane, wygląda to jak: "5866666666666666666666666666666666666666666666666666666666666666". Świetnie, z powrotem do bezużytecznych informacji.
• l: "kolejność" powyższego punktu bazowego. Jest to ważne, ponieważ określa maksymalną liczbę punktów, których możemy użyć, oraz maksymalny rozmiar, jaki mogą mieć nasze skalary. Ta liczba jest jak liczba "12" w zegarze; dodanie punktów lub skalarów razem, które "przeszłyby" oznacza, że zamiast tego "zawiną się". Gdybyś mógł dodawać G do siebie w kółko i w kółko, aż osiągnąłbyś l-1 liczbę dodawania, skończyłbyś z powrotem na G.
• Hs i Hp: s oznacza skalar, p oznacza punkt. Zostaną one omówione w późniejszym artykule.

Uwaga:

• Skalary (klucze prywatne, tak naprawdę po prostu duże liczby całkowite) są zawsze reprezentowane w równaniach małymi literami.
• Punkty (klucze publiczne, tak naprawdę zakodowane współrzędne na krzywej) są zawsze reprezentowane przez duże litery.

W praktyce zarówno klucze prywatne, jak i publiczne w Monero są reprezentowane przez 64 znaki heksadecymalne, podobnie jak powyższa reprezentacja G. Skalary są wprost reprezentowane jako liczby całkowite little-endian, podczas gdy punkty są specjalnie zakodowane w sposób, który jest zbyt skomplikowany dla tego artykułu.

Jeśli używamy x jako naszego klucza prywatnego i P jako naszego klucza publicznego, to P = xG.

Kilka "zabawnych" przykładów:

1. x = 1 lub "0100000000000000000000000000000000000000" (pamiętaj o little-endian); P = "5866666666666666666666666666666666666666" lub G. (1G = G)
2. x = l - 1 lub "ecd3f55c1a631258d69cf7a2def9de1400000000000000000000000000000010"; P = "58666666666666666666666666666666666666666666666666666666666666e6" (odnotuj podobieństwo z G); To jest ostatni punkt przed "zawinięciem". Możesz myśleć o tym jak o -G. Dodanie G do tej wartości spowoduje powstanie specjalnego elementu tożsamości, takiego samego jak pomnożenie punktu przez 0 lub odjęcie punktu od siebie.
3. Liczba całkowita (l+1) / 2, "f7e97a2e8d31092c6bce7b51ef7c6f0a000000000000000000000008", tworzy punkt najbardziej oddalony od G (wystarczająco blisko, ten i następny punkt są powiązane gdyż l jest nieparzyste), "ac1999070321b2c6309cc8e31aa89a8b3baa75b5f8febf47855555a3e744bcf0", podobnie jak 6 jest najdalej od 12 na zegarze. To (podobnie jak G i każdy inny punkt) ma punkt komplementarny (w tym przypadku produkowany przez (l-1) / 2), z którym będzie sumować się do elementu tożsamości.

Konta i adresy Monero

1. Wybierz losowy klucz prywatny, zwykle poprzez stworzenie 256 losowych bitów, a następnie "redukcję" mod l. Nazwij ten klucz b (aby dopasować się do whitepaper -- jest to mylące, wiem).
2. Hashuj b z wybranym algorytmem, H (Keccak_256 w naszym przypadku). Interpretuj wynik jako liczbę całkowitą i zredukuj ją mod l, jak poprzednio. Nazwij ten klucz a.
3. Oblicz B = bG i A = aG. To są twoje publiczne klucze wydawania i publicznego podglądu.
4. Hashuj (prefiks (0x12 w standardowym Monero) + B + A) z H.
5. Dodaj pierwsze cztery bajty wyniku do (prefiksu + B + A). Będzie to 69 bajtów (1 + 32 + 32 + 4).
6. Konwertuj na cnBase58. Nie jest to tak proste jak zwykła baza58, ponieważ używa bloków i paddingu, aby uzyskać konwersję o stałej długości. 69 bajtów zawsze będzie miało 95 znaków cnBase58.

Adresy zintegrowane są tworzone tak samo jak powyżej, ale z 8-bajtowym identyfikatorem płatności dołączonym do A w kroku 4 powyżej i innym prefiksem (0x13).